Kartenkunde

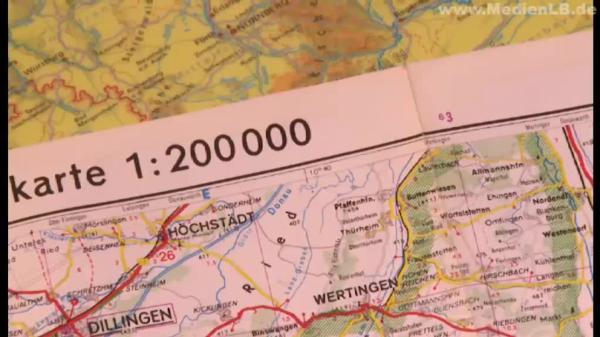
1. What Is a Compass and How Does It Work? Today, Arne and Jannis want to go hiking with their father. They are equipped with food, drinks and sturdy shoes. Original soundtrack son: “Dad, what’s that?” Original soundtrack father: “That’s a compass. We need it now so that when we don’t know the area, we can always see where north is and where the cardinal directions are. So that we can arrange your map in the right direction and use it properly. Look, there’s a compass symbol on it.” You’d like to know what a compass is. Let me explain: A compass is a measuring device with which you can identify the cardinal directions to get your bearings. But how does a compass work? The answer is: by magnetic force. When you place a magnet amidst metal filings, you can see how these filings are pulled to the magnet. And when you take a closer look, you can see that the filings arrange themselves in specific directions at the magnet. This way, you can see where the field lines of the magnet run. The horseshoe magnet has a north pole and a south pole like the Earth. The direction of the cuttings tells you where the field lines along these poles are. Just like the metal filings, the pointer of a compass is also pulled towards a magnet. If you move the magnet around the compass, you can see how the pointer follows the magnet. The movable pointer of the compass thus consists of a magnetic material and one of its tips is coloured red. This pointer is also called compass needle. It always points north. Our Earth, too, is a huge magnet with a north pole and a south pole. And, as with every magnet, with the Earth, too, field lines run from pole to pole. Just as we have just observed with the small magnet, the red magnetic compass needle is pulled towards the large magnetic field of our Earth’s north pole. Therefore, it always points north – no matter where you currently are on the globe. Therefore, you know at once where north is when you have a compass. Besides the movable compass needle, which tells you the north south direction, a compass also has other components. At the outer side, there is a rotatable scale ring with four cardinal directions. When you adjust the scale ring in such a way that the needle points to N, i.e. north, then you also know where the other cardinal directions are. You have to proceed clockwise: east, south, west. You can remember that with a mnemonic: Nobody enjoys stinging wasps. To determine the direction even better, there are intermediate cardinal directions. They are located between the main cardinal directions. Between north and east there is northeast. Between south and east there is south east. Between south and west there is south west and between north and west there is north west. All cardinal directions together are called wind rose. In order to determine the direction when you start, you orient the compass north. In doing so, you always have to hold the compass horizontally. The adjusting ring with the wind rose is turned until the N and the small triangle that indicates the walking direction coincide. Now turn the compass until the coloured tip of the compass needle points to N. Even if you don’t have a compass at home, you can find out where east, south west and north are. The sun will tell you. And a short poem will help you remember: In the east, the sun will start the day, then go along the southern way, till it will set in the west at night, in the north you'll never see its light. So you just check in the morning where the sun rises. Then you know where east is and you can get your bearings. 2. How Maps Are Created Arne, Jannis and their father use a map in addition to their compass in order to find their way in the unknown territory. Original soundtrack father: “Do you see a church there?“ Original soundtrack son: “Yes. Over there!” Original soundtrack father: “There’s a church. Oh, look! This seems to be the parking lot. Or that one, that depends ...“ But how is such a map created? If you’re standing on a hill, you have a good view of your surroundings. But it is difficult to draw a map of the landscape from there. There are things that you can’t recognize and the distances between villages are hard to estimate. Therefore, we’ll take a look at the same landscape from a different perspective. This picture of the mountain Jannis, Arne and their father are standing on has been taken from a plane. Here you can recognize the meadows, forests, the lake and the mountains like from a bird’s eye view: This is also called bird’s perspective. If you move farther away from the Earth’s surface to take a picture of the landscape from above, the view is getting wider. Such pictures, which are taken from satellites, can be simplified and transformed into a map. However, you should also know that land surveyors do the groundwork for the cartographers. They have to check exactly how far the distance actually is between places or other objects. Then all indications you later see on your map are correct. Original soundtrack land surveyor: “Staking-out: 22 m from the instrument …” While maps used to be drawn by hand in the past, today computer programmes assist in the drawing of maps. In this company, which produces maps for schools in Austria, we will experience how a map of the Austrian city of Graz and its surroundings is created. The data that have been previously gathered via satellites and by land surveyors can be appropriately processed here. Depending on the purpose and kind of the map to be drawn, towns, roads, forests or watercourses are depicted in a way that the viewer can easily comprehend the map. For a better general understanding, specific colours have been agreed on for the illustration of maps. Streets and roads, for instance, are usually depicted in yellow, red or white. Water is marked by blue. Inhabited areas, like the urban area of Graz, are depicted in light red, forests, parks and meadows in light green. Mountains are rendered in shades of brown, the darker the brown is the higher is a mountain. Lower areas are depicted in beige or, farther down, in green again. The boundary lines of districts within Austria are exactly marked on the maps. Symbols are used for churches, camping sites, sights or other special places. The names of towns, rivers and lakes are also indicated on maps. In addition, all colours and symbols as well as their meanings are explained in a legend on the map. Thus, a map is created with the help of data obtained by satellites and surveying. It contains different colours, lines, names and symbols. The meanings of these elements are explained in a legend. Let’s summarise: A map is like a photo from above – from the bird’s eye view – but in the form of a drawing. It is a scaled-down and simplified picture of the landscape. There are different kinds of maps that differ from each other according to their type and the purpose they’ve been made for. There are hiking maps, road maps or nautical charts for the navigation of ships. But you can also depict other things on maps. If, for instance, we wish to know how the climate zones of the world are distributed, a world map which includes the different temperature zones might help us. Such topic-based maps can have highly different contents – for instance, the division of a federal state into districts or the distribution of religions in the world or the different vegetation zones of our planet, and many more topics. 3. Reading a Map – No Problem You can read a map almost like a book and this way, you will learn a lot about the territory shown. When you are in an area you are not familiar with, then it will be easier for you to find your way if you know how to read a map. To do so, we can choose from different kinds of maps – depending on the purpose they are intended for. Car drivers use other maps than pedestrians. Maps like this – they are also called topographic maps –are useful when you want to get your bearings in the countryside. These maps tell you whether the terrain is flat or mountainous and the course of rivers and trails. With maps like that, you can easily prepare a hiking tour and orientate yourself on your way. Original soundtrack father: “Now let’s see. Good thing we know where we are.” It is not that difficult to read a map. You just have to know a few graphic elements. Firstly, you have to know how a map is oriented. This means where the cardinal directions are. Our modern maps of today are already oriented north. This means that the cardinal directions are always in the same place – on any map. Thus, north is always at the top. East is on the right. South is at the bottom. West is on the left. If you have a compass with you, you can orient the map in such a way that it is aligned with the cardinal directions in real life. That can help with orientation, to know where you are and what you see. Original soundtrack father: “Now it has the correct position, to the north.“ Original soundtrack son: “So we’re looking north.” Original soundtrack father: “This is north. And now the map is aligned with its north orientation.” Original soundtrack son: “Then south should be there.” Original soundtrack father: “South is there. Look! North, east, south and west. Where does the sun set? In the west.” When you look closely, you will see that numbers are printed on the cover or the margin of a map. They will say 1:50,000, 1:250,000 or 1:2,100,000 or something similar. But what do these numbers mean? They indicate the scale of a map. The scale is always indicated as a numerical ratio. On the map, it reads e.g.: 1:200,000. This means that 1 cm on the map corresponds to 200,000 cm in real life. Now we convert these numbers: 200,000 cm are 2,000 m and 2,000 m are 2 km. Thus, the scale of 1:200,000 means that 1 cm on the map is 2 km in real life. On the map, these two places are 6 cm apart from each other. With our scale of 1:200,000 these are actually 12 km. Hence, the scale describes the ratio between the map and the real conditions in centimetres. If you wish to know what a landscape that stretches across a long distance looks like, you need a map with a small scale, like here, for instance, a map of western Austria with a scale of 1:400,000. Thus, a small-scale map shows a larger area. They represent even large cities just as dots. On the other hand, for orientation around a city, like here with the city of Graz in southwestern Austria, you need a map with a larger scale like this one with 1:120,000. The area shown on this map is smaller, but all the items you can see on a map are displayed larger. You surely also want to know the meaning of these lines on the map. Since a map is drawn with a view from above, you can of course not recognise mountains. In order to illustrate the different levels of elevation in a landscape on a map, lines are shown, each of which corresponds to a certain height level. If you draw lines around this mountain at specific height intervals, a pattern is created with which you can also read whether the terrain is flat or steep when it is viewed from above. The closer the lines are together, the steeper is the mountain. The farther the lines are apart, the flatter is the terrain. On a map, the distances between the contour lines are marked with colours. In this way, you can read the exact levels of elevation in the legend. 4. Reading Aids for Maps In order to “read” a map properly, you have to know its legend. In the legend, which you usually find on the margin of the map, all symbols and colours depicted on the map are explained. It is said: The legend is the ABC of a map. On this map of Bavaria, there are a number of different colours, lines, signs and symbols. In the legend of the map, all these elements are explained. For instance, you can learn from the different font sizes used for the city names how many people live there. In the legend, it is also explained how the different height levels of the map are marked with colours. You can clearly see that the Alps with their high mountains are marked in brown to dark brown and that the lower lands in Bavaria, such as, for example, the river course of the Danube, are marked in green. But also the different lines on the map, which stand for roads or railway lines or for the course of boundaries and rivers, may be found in the legend. Finally, there are special places like a fen, a mountain pass, an airport, a monastery or a castle, whose representation as a symbol is explained in the legend of a map. On other maps, such as, for instance, with the town map of Manching near Ingolstadt, other items are depicted and explained in the legend. Here the symbols mainly indicate special sites on the town map. A symbol is easy to recognise on a map. In addition, symbols take up considerably less space on the map than writing. If you wish to find, for example, the post office in Manching, you check in the legend what the symbol for the post office looks like. Next, you simply search for the symbol for the post office on the map. Then you’ll know where the post office is in Manching. The distribution of areas is also explained in the legend. With the explanation of the colours in the legend, you will see at one glance on the map where there is a forest or a business park. The scale of the map is often also indicated in the legend. Here you can see that the scale is 1:18,000. As you have seen, not all symbols and colours are the same on all maps. They depend on the purpose the map is intended for. For this reason, each map has its own explanation of symbols – the legend. You need it to be able to read a map precisely and correctly. Marie, Anna and Max are moving through an unfamiliar city with their mother. The weather is nice, so they want to go to the park. But how do you find the way to the park? In order to find your destination also in unfamiliar cities, there are city maps. On a city map, all streets, buildings, parks and squares are indicated. With the help of a street directory, you can find every street on the map. The street directory is a long list that includes all streets of a city. But what is the meaning of the letters and numbers after each street name? They help us to find streets and buildings. Original soundtrack mother: “And what’s the number?” Original soundtrack children: “L10.” Original soundtrack mother: “Now we have to unfold it here.” “Now look where we have to go!” Grids are superimposed on every city map. A grid consists of square fields that are called grid squares. Each square has a distinct denomination by means of the capital letter on the upper margin and the number at the side. The suburban train station where the children got off with their mother is in grid square L9. The park is in grid square L10. Their way to the park thus leads them across two squares. In order to ensure that they are walking into the right direction, they check their map from time to time during their walk and compare the street signs at the crossroads with the street names on their map. You see, it’s not that difficult to find your way with a street-map. Now you can practise it, too! Original soundtrack father: “Now look, we’re just about right with the map. This one almost points north ...” A map and a compass help us to orient ourselves more easily in the world. If you know how a compass works, you can anytime and anywhere determine where north, east, south or west are and in which direction you are moving. For you to get your bearings when hiking or in a city and to know where you are at the moment, there are maps. If you have a map with the right scale and also know how to use a street directory or the symbols in the legend, then you have an important aid for being out and about in the world.